
Tweet
| Navigation |
| Home |
| Site map |
| Articles |
| Contact |
| Links |
| Forum |



Getting a flat base on a 3 frequency domeIf a 3v dome were cut in half the dividing line wouldnít be exactly half a dome, take a look at the diagram below. The blue line shows the line that would divide a sphere exactly in half, this line cuts through all the base triangles and isnít really a satisfactory way of finishing the bottom of a dome, so what most people do is decide if they need a taller or shorter dome and cut the dome at the red line for a 4/9 dome or the green line to create a 5/9 dome. 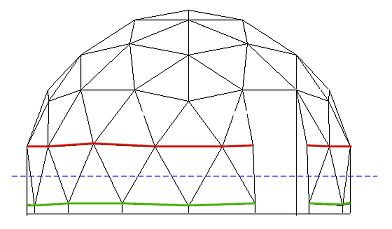 This all sounds fine but weíre left with a problem to solve. The dividing line at the 4/9 and 5/9 cut is now not straight so the dome wonít sit flat on the ground. There are a number of ways to solve this including adjusting the strut lengths on the bottom triangles, using a fillet and changing the dome orientation, Iím not keen on changing strut lengths as it adds complexity to an otherwise simple design so Iíll explore the later two as possible solutions. Adding a fillet A simple fix is to add a tapered fillet that makes up the difference required to make the base flat. On a 4.5 meter dome this is 35mm so you would need a fillet that runs from nothing to 35mm fitted on every hex base strut (Strut Ďcí on the dome calculator) for a 4/9 dome. On a 5/9 dome a solid base is added because the 35mm slope is going the opposite direction cutting a 35mm to nothing sliver off the base beam is needed, the diagram below shows a dome laid out horizontally to better demonstrate which struts need packing. 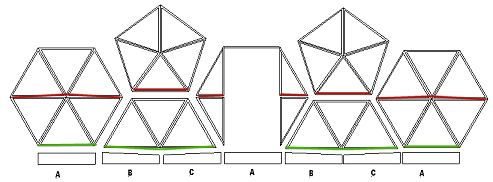 Changing the dome orientation Another fix for this problem is to simply rotate the dome until a convenient dividing point is reached. Some of the base triangle will need to be cut in half but this is still much easier than changing strut lengths. The diagram below shows a 3v dome that has been rotated 90 degrees then divided along a line exactly through the centre, this solution has the added benefit of producing an exact half sphere. 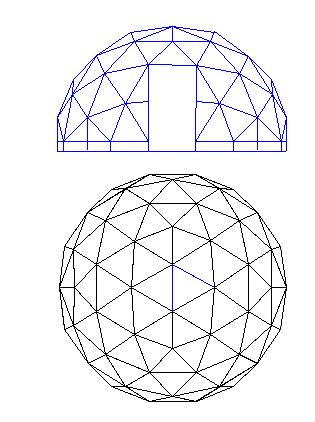 |
|
 |
|
| [ comments 8 ] |
| posted by Colin | 15/12/2008 20:59:15 |
 |
|
| It would be a good method for a panel dome as making triangles is more labour intensive. For a hub and strut its just as easy to cut the extra strut lengths. Adjusting the end stop to set the cut off length doesnt take more than a few seconds :) | |
 |
|
| posted by Rob | 13/05/2009 23:11:29 |
 |
|
| I am planning to construct a small lean-to greenhouse with a height of 2metres. How can I design it as a 1/4 sphere (if that is the right term.....I am a complete novice as far as domes are concerned) with straight edges for fixing to the ground and the back wall? Material for construction will be 2x1 timber using hub and strut method. | |
 |
|
| posted by simon | 14/05/2009 21:23:39 |
 |
|
|
Hi Rob There's lots of ways to do a quarter sphere. Which you choose is a combination of what you want it to look like and which of the various complications you're more comfortable with. An icosa dome has a minimal number of parts, but you'll need some custom work because it doesn't naturally cut into a quarter sphere, although it's only a matter of dividing facets in half. The 3v has managably small panes, but it won't be twice as long as high because it doesn't sit on a mid-plane, which also means you need a small amount of packing to sit it down flat. Both the 2v and 4v sit flat on a mid plane, but the 2v isn't as pretty and the 4v is a little more complicated. An octa dome splits naturally into a quarter sphere so there's no custom hubs with tight angles and you might prefer how it looks as a lean-to, but it has a much greater varity of strut length and pane size so in that respect it's more complicated than an equivelent icosa. |
|
 |
|
| posted by Rob | 18/05/2009 02:50:55 |
 |
|
| Thanks Simon. Have been busy with cardboard and glue making models of various designs. Trying to get a something that does not have too shallow an angle on the walls.....perhaps I should go for more than 1/2 diameter for the height? Sorry to show my ignorance but what is the difference between icosa and octa. | |
 |
|
| posted by simon | 21/05/2009 11:59:07 |
 |
|
|
Hi Rob Geodesic domes are mostly based on the 20-sides icosahedron, and its equilateral triangular faces are divided up into smaller facets - the frequency of the dome tells you how - 2v gives 4 facets, 3v gives 9, etc - and then the corners of those facets are all projected out to the same radius to make a sphere. An icosahedron is a good basic solid because it already has 20 faces and that makes icosa domes rather efficient. But the principle works for any platonic solid - tetrahedron, cube, octahedron and dodecahedron too. The down-side with the icosa dome for your design is that the icosahedron doesn't have orthogonal axes of rotational symmetry so it doesn't split into a quarter-dome along its struts, whereas the octahedron does. Here's a picture (Sorry Paul, can you in-line it?) 
|
|
 |
|
| posted by gravitonium | 08/07/2009 22:48:57 |
 |
|
| we are able to generate any dome? with flat base in 3 rd and other frequencies, using more or less than the half. We are also capable of generating the calculations for ellipsoids and egg like structures, or using any sector and height. We'll be glad to help you... | |
 |
|
| posted by Marc | 02/02/2011 22:54:13 |
 |
|
| Hi everyone! Does anybody know how to calculate the fillet height (to get a flat base)for any given radius of a 3V dome? I mean, using a formula rather than 3D cad. Thanks! | |
 |
|
| posted by Admin | 07/02/2011 23:20:30 |
 |
|
|
Hi Mark, I use this formula: Take the radius of the dome ( in millimeters) and divide it by 67.77 this will give you the height of the fillet required in millimeters. You'll need to take off this amount for a 5/9th dome. |
|
 |
|
comments will be accessed through the forum in the new site design (coming soon)
8859
Copyright © 2007- 2014 geo-dome.co.uk. All Rights Reserved.