
Tweet
| Navigation |
| Home |
| Site map |
| Articles |
| Contact |
| Links |
| Forum |



Geodesic dome frequency explained
To increase the frequency we have to do two things, first subdivide a face into more triangles then project out the vertex of each triangle to an imaginary sphere encompassing the dome. See diagram below:  Higher frequency domes just have more subdivisions; the diagram below shows how 1v, 2v, 3v, and 4v spheres are subdivided. Notice how only even frequencies have a dividing line exactly across the centre of a sphere, while odd frequency spheres have to be divided slightly above or below the centre line. This is why 3v domes don’t have a flat base and come in 4/9th or 5/9th versions. 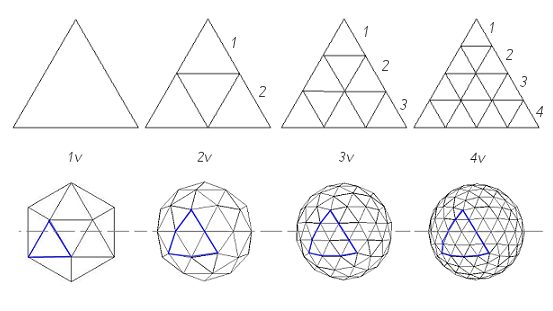 The greek letter for Phase or frequency is Nu or Nv written N in latin the lowercase (ν) is used as the symbol for spatial frequency of a wave in physics and other fields, a measure of how often components of a structure repeat per unit of distance. Basically the v in 3v stands for frequency. OK now that you know a little about dome frequency take a look at the dome below and work out what frequency it is. If you need a clue…Find the centre of a pentagon and count how many struts there are to the centre of any other pentagon. Click the image to find the answer.  Related pages: |
|
 |
|
| [ comments 0 ] |
comments will be accessed through the forum in the new site design (coming soon)
11849
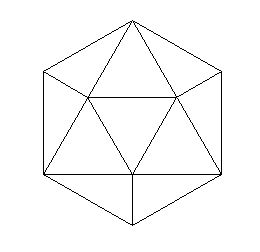 We will start with an icosahedron, as most geodesic domes are based on this basic form. Icosahedrons have 20 equilateral triangle faces that form very roughly a sphere. If you look at the example you will notice that all the struts are the same length and all the triangles are the same size, quite a beautifully simple start point for building a dome. All frequency domes can be traced back to this basic form, which can be classed as a 1v geodesic sphere.
We will start with an icosahedron, as most geodesic domes are based on this basic form. Icosahedrons have 20 equilateral triangle faces that form very roughly a sphere. If you look at the example you will notice that all the struts are the same length and all the triangles are the same size, quite a beautifully simple start point for building a dome. All frequency domes can be traced back to this basic form, which can be classed as a 1v geodesic sphere.